95.501

2000

4 Building Abstractions with Data

What's in This Set of Notes ?

Introduction
Abstraction
Pairs
Abstraction Barriers
What is Meant by Data
Representing Sequences
Hierarchical Structures
Symbolic Data

4.1 Introduction

Review (essence of Programming)

Computational processes

iterative process
recursive process

Role of procedures in program design
Primitive data (numbers)
Primitive operations (arithmetic)
Combining Procedures to form compound procedures

composition
conditional

Use of parameters
How to abstract procedures with define
How to enhance language with higher-order procedures

Focus

Want to build abstractions by combining data objects to form compound data

Why? (same reasons for compound procedures)

to elevate the conceptual level at which we design programs

increase modularity of design

enhance expressive power of language

4.2 Abstraction

Data Abstraction

Methodology that enables us to isolate how a compound data object is used from the details of how it is constructed from more primitive data objects, enabling one to replace/swap/switch implementations.

Interface between two parts of system (user and developer) will be a set of procedures called selectors and constructors

Procedural Abstraction

Separate the way the procedure would be used from the details of how the procedure is implemented in terms of more primitive procedures, enabling one to replace/swap/switch implementations

Example: Rational Numbers

n1/d1 + n2/d2 = (n1d2 + n2d1) / (d1d2)
n1/d1 - n2/d2 = (n1d2 - n2d1) / (d1d2)
n1/d1 * n2/d2 = (n1n2) / (d1d2)
(n1/d1)/ (n2d2) = (n1d2) / (n2d1)
n1/d1 = n2/d2 if and only n1d2 = n2d1

Assume you has the following constructors and selectors:

(make-rational ?n ?d) returns a rational number with numerator ?n and denominator ?d

(numerator ?x) returns numerator of rational number ?x

(denominator ?x) returns denominator of rational number ?x

(define (add-rational x y)
    (make-rational (+ (* (numerator x) (denominator y))
                                (* (numerator y) (denominator x)))
                            (* (denominator x) (denominator y))))

(define (subtract-rational x y)
    (make-rational (- (* (numerator x) (denominator y))
                                (* (numerator y) (denominator x)))
                            (* (denominator x) (denominator y))))

(define (multiply-rational x y)
(make-rational (* (numerator x) (numerator y))
(* (denominator x) (denominator y))))

(define (divide-rational x y)
(make-rational (* (numerator x) (denominator y))
(* (denominator x) (numerator y))))

(define (equal?-rational x y)
(= (* (numerator x) (denominator y))
(* (numerator y) (denominator x))))

How do we glue together numerator and denominator to represent rational number?

However, notice that we can use rational numbers even though we don't know anything about how they are structures
The answer is Pairs

4.3 Pairs

A pair (sometimes called a dotted pair) is a record structure with two fields called the car and cdr fields (for historical reasons).
Pairs are created by the procedure cons.
The car and cdr fields are accessed by the procedures car and cdr.
The car and cdr fields are assigned by the procedures set-car! and set-cdr!

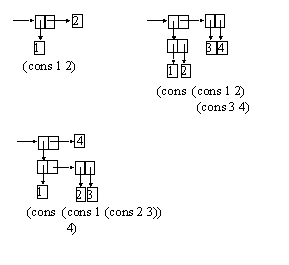
(cons 1 2) => (1.2) // . only for display
(define x (cons 1 2))
(car x) => 1
(cdr x) => 2
(define y ( cons 3 4))
(cons x y) => ((1.2) 3 . 4) //Think of pairs as a single object
(define z (cons x y))
(car z) => (1.2)
(car (car z)) => 1
(car (cdr z)) => 3

Pair Visualization: Box and Pointer Notation

Closure

A package of function and variable bindings is called a closure. This term derives from the idea that the packaged functions are now "closed" to the state of the outside world - they can be used in any environment, independent of the bindings that exist in that environment, because all of the identifiers they uses are bound either to arguments, local variables, or the closure's external bindings.

Closure Property

an operation (like cons) for combining data objects satisfies the closure property if the results of combining things with the operation can themselves be combined using the same operation

Representing rational numbers with Paris

(define (make-rational numerator denominator)

(cons numerator denominator))

(define (numerator rational)

(car rational))

(define (denominator rational)

(cdr rational))

Using Rationals

(define one-third (make-rational 1 3))
(add-rational one-third one-third) => (6.9)

Must fix problems with display

should not show dot notion

should reduce rational to lowest terms

(define (print-rational x)
    (newline)
    (display (numerator x))
    (display "/")
    (display (denominator x)))
(print-rational (add-rational one-third one-third)) => (6 / 9)
(define (make-rational numerator denominator)
    (let (( g (gcd numerator denominator))))
        (cons (/ numerator g) (/ denominator g))))
(print-rational (add-rational one-third one-third)) => (1 / 3)

4.4 Abstraction Barriers

abstraction barriers isolate different levels of the system

--- (Programs that use rational numbers) ---

rational numbers in problem domain

---- (add-rational , subtract-rational , ...) ---

rational numbers as numerators and denominators

--- (make-rational, numerator, ...) ---

rational numbers as pairs

--- (cons, car, cdr) ---

however paris are implemented

--- lines represent abstraction barriers
barrier separates the program above that uses the data abstraction from the program below that implements the data abstraction
each level is the interface
For data abstraction

identify type of data objects
identify basic set of operations
use only those operations

makes programs easier to maintain and modify later

(define (numerator rational)

(let ((g (gcd (car rational) (cdr rational))))

(/ (car rational) g)))

4.5 What is Meant by Data

More than just selectors and constructors
More than just arbitrary set of procedures
Must also specify conditions that these procedures must fulfill in order to be a valid representation
E.G.

If x is (make-rational numerator denominator)

Then

(numerator x)/ (denominator x) = numerator/denominator

Same can be said for pairs

If z is (cons x y)

Then

(car z) = x and

(cdr z) = y

Therefore, any triple of procedures can provide basis for pairs

4.6 Representing Sequences

List Structure

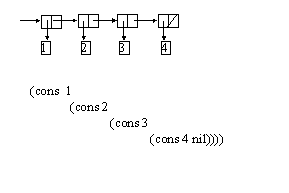
Instead of cons use list primitive

(list ?a1> ?a2> ... ?an>) which is equivalent to (cons ?a1> (cons ?a2> ( .... (cons ?an> '()))))

Note: #f, nil, and '() are all the same

(define one-to-four (list 1 2 3 4))

(car one-to-four) => 1

(cdr one-to-four) => (2 3 4)

(cons 10 one-to-four) => (10 1 2 3 4)

List Operations

Problem: Find nth element in list?

(define (get-element items n)

(if (= n 0)

(car items)

(get-element (cdr items) (- n 1))))

Technique know as cdring down

(define squares (list 1 4 9 16 25))

(get-element squares 3) => 16

Problem: Append two lists together?

(define (append list1 list2)
    (if (null? list1)
        list2
        (cons (car list1)
                (append (cdr list1) list2))))

Technique know as consing up

(define odds (list 1 3 5 7 9))
(append square odds) => (1 4 9 16 25 1 3 5 7 9)

Problem: Scaling numbers?

(define (scale-list items factor)
    (if (null? items)
        nil
        (cons (* (car items) factor)
                (scale-list (cdr items) factor))))
Technique know as mapping over lists
(scale-list (list 1 2 3 4 5 ) 10) => ( 10 20 30 40 50)
Abstracting the general idea to capture a common pattern expressed as a higher-order procedure
(define (map procedure items)
    (if (null? items)
        nil
        (cons (procedure (car items))
                (map procedure (cdr items)))))
(map abs (list -10 2.5 -11.6 17)) => (10 2.5 11.6 17)
(map (lambda (x) (* x x)) (list 1 2 3 4)) => ( 1 4 9 16)

Problem: Selecting numbers?

(define (filter predicate sequence)
    (cond ((null? sequence) '())
                ((predicate (car sequence)) (cons (car sequence) (filter predicate (cdr sequence))))
                (else (filter predicate (cdr sequence)))))
Technique know as filtering over lists
(filter odd? (list 1 2 3 4 5 6 7)) => ( 1 3 5 7)

Problem: Summation of numbers?

(define (accumulate operator initial sequence)
    (if (null? sequence)
        initial
        (operator (car sequence) (accumulate operator initial (cdr sequence)))))
Technique know as accumulating over lists
(accumulate + 0 (list 1 2 3 4 5)) => 15
(accumulate * 1 (list 1 2 3 4 5)) => 1200

Problem: How to combine mapping and accumulating?

(define (flatten-map procedure sequence)
(accumulate append nil (map procedure sequence)))
(map list (list 1 2 3)) => ( (1) (2) (3))
(flatten-map list (list 1 2 3)) => ( 1 2 3)

4.7 Hierarchical Structures

Lists generalize to represent sequences whose elements may themselves be sequences (trees)

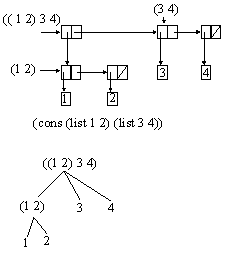
Recursion is a natural tool for dealing with trees

(define (count-leaves tree)

(cond ((null? tree) 0)

((not (pair? tree)) 1)

(else ( + (count-leaves (car x))

(count-leaves (cdr x))))))

4.8 Symbolic Data

Suppose we want (a b)
Can't use (list a b) because list will evaluate a b first
In order to manipulate symbols we need the ability to quote a data object
Quotation marks indicate that a word or sentences is to be treated literally as a string of characters
Scheme follows the same practice to identify lists and symbols
The meaning of single quote character is to quote the next object
Quote also allows us to type in compound objects

(define a 1)

(define b 2)

(list a b) => (1 2)

(list 'a 'b) => (a b)

(list a 'b) => (1 b)

(list 'me 'you) => (me you)

(car '(a b c)) => a

(cdr '(a b c)) => (b c)

Violates general rule that all compound expressions should be delimited by ().
Therefore special form quote is added
(quote a) and 'a are equivalent, as is (quote ( a b c)) and '(a b c)