3  Building Abstractions with Procedures

What's in This Set of Notes ?

• Conditional Expressions and Predicates
• Procedures and The Processes They Generate
• Other Forms of Recursion
• Procedures
• Summary

• Following construct is called case analysis

|x| =         x if x>0
                0 of x = 0
               -x if x <= 0

• Requires special form called cond

(cond   ( <p1> <e1>)
            ( <p2> <e2>)
            ...
            ( <pn> <en>))

• Expression of the form ( <p> <e>) is called a clause
• First expression in clause is called a predicate, e.g. whose values is either true or false

(define (abs x)
    (cond    (( > x 0) x)
                (( = x 0) 0)
                ((< x 0) (- x))))

• Another way

(define (abs x)
    (cond    (( < x 0) (- x))
                (else x)))

• Another way

(define (abs x)
        (if (< x 0)
            (- x)
            x))

• Requires special form called if

(if  <predicate> <consequent> <alternative> )

• Primitive Predicates: <, = , >

• Logical Composition Operations

(and <e1> ...  <en>)  evaluate left to right, as soon as one expression is false return false

(or <e1> ...  <en>) evaluate left to right, as soon as one expression is true return true

(not <e>)

(define (>= x y)
     (or ( > x y) (= x y))

(define (>= x y)
    (not (< x y))

Example: Compute Square Roots using Newton's method of successive approximations

1. guess y for value of square root of number x
2. to get a better guess average y with x/y

(define (good-enough guess x)
    (< (abs (- (square guess) x)) 0.001))

(define (average x y)
    (/ (+ x y) 2))

(define (improve guess x)
    (average guess ( / x guess)))

(define (sqrt-iteration guess x)
    (if (good-enough? guess x)
            guess
            (sqrt-iteration (improve guess x) x)))

(define (sqrt x)
    (sqrt-iteration 1.0 x))
 

Sqrt is first example of process defined by a set of mutually defined procedures

Problem breaks up naturally into subproblems: decomposition strategy

Details of how sqrt is computed can be hidden (black box) creating a so-called procedural abstraction

Take the procedure square, we know what we want, but how does it do it?

 
(define (square x) ( * x x))

(define (square x) (exp (double (log x))))

(define (double x) ( + x x ))

A procedure definition should be able to supress details

Users of procedure may not have written it

Users should not need to know how a procedure is implemented in order to use it!

---

Local names

• Formal parameter of procedure has special role, it doesn't matter what  name of the formal parameter has
• such a name is called a bound variable, the procedure definition binds its formal parameters
• the meaning of the procedure definition is unchanged if the name of bound variable is consistently renamed
• If variable not bound, is free
• The set of expressions for which a binding defines a name is called the scope of the name

• How to hide choice of procedure names from users of sqrt?
• Allow procedure to have internal definitions local to procedure
• Such nesting of definitions is called block structure
 
Developers view of sqrt procedure

(define (sqrt x)

    (define (good-enough guess)
            (< (abs (- (square guess) x)) 0.001))

    (define (improve guess)
            (average guess ( / x guess)))

    (define (sqrt-iteration guess)
            (if (good-enough? guess x)
                guess
                (sqrt-iteration (improve guess x) x)))

    (sqrt-iteration 1.0))
 

Users view of sqrt procedure

(define (sqrt x) ....)

User cannot directly use procedures good-enough, improve and sqrt-iteration
 

• Note, x is now a free variable. x gets its value from the argument with which the enclosing procedure sqrt is called
• This is called lexical scoping

• A procedure is a pattern for the local evolution of a computational process
• What to make statements about the overall/global behavior of the process (difficult)
• To become experts, we must learn to visualize the processes generated by various types of procedures.

---

Factorial function

 
n! = n * (n - 1) * (n - 2) . . . 3 * 2 * 1
n! = n * (n - 1)!

---

Linear Recursive Process

(define (factorial n)
    (if ( = n 1)
        1
        (* n (factorial ( - n 1)))))

Substitution Model for (factorial 5)

(factorial 5)
(* 5 (factorial 4))
(* 5 (* 4 (factorial 3)))
(* 5 (* 4 (* 3 (factorial 2))))
(* 5 (* 4 (* 3 (* 2 (factorial 1)))))
(* 5 (* 4 (* 3 (* 2 1))))
(* 5 (* 4 (* 3 2)))
(* 5 (* 4 6))
(* 5 24)
120

This is a linear recursive process

• expansion followed by contraction
• chain of deferred operations (*)
• interpreter keeps track of operations to perform later
• amount of information to keep track of grows linearly

---

Linear Iterative Process

(define (factorial n)
    (factorial-iteration 1 1 n))

(define (factorial-iteration product counter maximum)
    (if (> counter maximum)
        product
        (factorial-iteration (* counter product) (+ counter 1) maximum)))

Substitution Model for (factorial 5)

(factorial 5)
(factorial-iteration 1 1 5)
(factorial-iteration 1 2 5)
(factorial-iteration 2 3 5)
(factorial-iteration 6 4 5)
(factorial-iteration 24 5 5)
(factorial-iteration 120 6 5)
120

This is a linear iterative process

• state can be summarized by a fixed number of state variables together with a rule on how to update them
• end test is optional
• number of steps grows linearly

---

Comment

• The above procedures are recursive (the procedure syntactically refers to itself)
• Don't confuse this with the notion of a recursive process (how computation evolves)
• Ada, Pascal and C are designed in such a way that recursive procedures consume an amount of memory that grows with the number of procedure calls
• Ada, Pascal and C therefore require special looping constructs (repeat-until, while, for)
• Scheme executes an iterative process in constant space (this property is called tail-recursive)

Tree Recursion

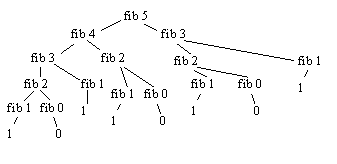
Fibonacci Numbers

Fib(n) = 0                                        if n = 0
Fib(n) = 1                                        if n = 1
Fib(n) = Fib(n - 1) + Fib(n - 2)        otherwise

0, 1, 1, 2, 3, 5, 8, 13, 21 ....

---

Recursive Process

(define (fib n)
    (cond (( = n 0) 0)
                (( = n 1) 1)
                (else
                    (+ (fib (- n 1))
                        (fib ( - n 2))))))

process looks like a tree

inefficient due to duplicate computation

 

---

Iterative Process

(define (fib n)
    (fib-iteration 1 0 n))

(define (fib-iteration a b count)
    (if (= count 0)
            b
            (fib-iteration ( + a b) a (- count 1))))

(fib 4)
(fib-iteration 1 0 4)
(fib-iteration 1 1 3)
(fib-iteration 2 1  2)
(fib-iteration 3 2  3)
(fib-iteration 5 3  0)
3

• We have seen that procedures are abstractions that describe compound operations on numbers independent of the particular numbers
• Used to express general methods of computation independent of functions
• Using only  numerical processing we will severely limited our ability to create abstractions
• Want to be able to do the following:
• build higher order procedures
• assign names to them
• work with them

---

Procedures as Arguments

• Compute the sum of integers from a through b

(define (sum-int a b)
    (if (> a b)
        0
        (+     a
                (sum-int (+ a 1) b))))

• Compute the sum of cubes from a through b

(define (cube x) (* x x x ))

(define (sum-cubes a b)
        (if ( > a b)
            0
            (+ (cube a)
                (sum-cubes (+ a 1) b))))
 

Compute (1/(1 * 3)) + (1/(5 * 7)) + (1/(9 * 11)) + . . .   converges to pi/8

 

 
 
 
 
 
 
 
 
 

(define (pi-sum  a b)
        (if ( > a b)
            0
            (+  (/ 1.0 (* a (+ a 2))
                    (pi-sum (+ a 4) b))))

• There is a pattern here:

(define (<name> a b)
    (if ( > a b)
        0
        (+ (<term> a)
            (<name> (<next> a) b ))))

(define (sum term a next b)
    (if ( > a b)
        0
        (+ (term a)
            (name (next a) b ))))
 

• Let's redo our sum-int and sub-cubes example
• First we must define term and next functions for our examples

(define (inc n) (+ n 1))
(define (identity n) n)

(define (sum-int a b)
    (sum identity a inc b))

(define (sum-cubes a b)
    (sum cube a inc b))

(define (pi-sum a b)
    (define (pi-term x) (/ 1.0 (* x (+ x 2))))
    (define (pi-next x) ( + x 4))
    (sum pi-term a pi-next b))
 

---

Special form Lambda

• Want to be able to create unnamed procedures
• More convenient than defining trivial procedures such as pi-term and pi-next
• Use special form lambda

(lambda (<formal parameters>) <body>)
 

(lambda (x) (+ x 4)) returns a  procedure that increments x by 4 like pi-next
(lambda (x) (/ 1.0 (* x (+ x 2)))) returns a  procedure that is like pi-term
 

(define (plus4 x) (+ x 4)) is equivalent to (define plus4 (lambda (x) (+ x 4)))

Note: Evaluating a lambda expression returns a procedure object

Therefore:
 

((lambda (x) (+ 1 x)) 2) => 3

in the same way:

(define (increment x)
        (+ 1 x))
(increment 2) => 3

or

(define increment (lambda (x) (+ 1 x)))
(increment 2) => 3

---

Using Lambda to create local variables

f(x,y) = x(1 + xy)(1 + xy) + y(1 -y) + (1 + xy)(1 -y)

if a = 1 + xy and b= 1-y

f(x,y) = xaa + yb + ab

(define (f x y)
    (define (f-helper a b)
        (+     (* x (square a))
                (* y b)
                (* a b)))
    (f-helper (+ 1 (* x  y))
                    (- 1  y)))

(define (f x y)
    ((lambda a b)
            (+     (* x (square a))
                    (* y b)
                    (* a b)))
        (+ 1 (* x  y))
        (- 1  y)))

---

Special form Let: Syntactic sugar for Using Lambda to Create Local Variables

The syntax for lambda
 

((lambda (<var1> ...<varn>)
    <body>)
<exp1>
<exp2>
.
.
.
<expn>)

(let ((<var1> <exp1>)
        (<var2> <exp2>)
        .
        .
        .
        (<varn> <expn>))
    <body>)

let <var1> have the value <exp1> and
    <var2> have the value <exp2> and
    .
    .
    .
    <varn> have the value <expn> and
in <body>

(let ((x 3)
        (y (+ x 3)))
    (* x y))

=> with generate the value 12 when evaluated

Note: Scope of variables is in let expression
Therefore:
 

(define x 5)
(+     (let (( x 3))
            (+ x (* x 10)))
        x)

=> 38

(define (f x y)
    (define a (+ 1 (* x y)))
    (define b (- 1 y)
    (+     (* x (square x))
             ( * y b)
             (* a b))))
 
• You should save define for binding procedures to a name
• When you need temporary variable bindings, use let

 

 
 
 
 
 

(define (f x y)
    (let (( a (+ 1 (* x y)))
            ( b (- 1 y)))
        (+     (* x (square x))
             ( * y b)
             (* a b))))

---

Quiz

(define (f g)
    (g 2))

(f square) =>?   4 is the answer

(f (lambda (z) (* z (+ z 1)))) =>?  6 is the answer

(f f) => ?  we will get an error by attempting to evaluate 2 as a procedure, the trace is as follows

(f f)
(f 2)
(2 2)

---

Procedures as Return Values

(define (average-damp f)
    (lambda (x) (average x (f x))))

Applying average-damp to the square procedure returns a procedure whose value when evaluated is the average of x and x squared

((average-damp square) 10) => 55

• Procedures
• named by variables
• passed as arguments to procedures
• returns as results from procedures
• procedures can be created with lambda
• lambda can be used to create local variables
• let is syntactic sugar for lambda