| Foundations of Programming Paradigms |
2000 |
8
Programming With Prolog
|
What's in This Set of Notes ?
| 8.1
Meaning of Prolog Programs |
Declarative Meaning
-
determines whether a given goal is true, and if so, for what
values of variables it is true
-
formally, given a program P and a goal G, the declarative
meaning says:
A goal G is true (that is, satisfiable, or logically
follows from the program) if and only if
-
There is a clause C in the program such that
-
there is a clause instance I of C such that
-
the had of I is identical to G, and
-
all the goals in the body of I are true.
-
Consider the following problem of representing the general
notion of a good apartment:
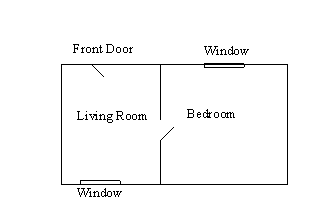
-
Any good architect would design an apartment with the following
rules in mind.
-
The living room window should be opposite the front door
to create a feeling of space
-
The bedroom door should be in one of the walls at right angles
to the front door to provide a little privacy
-
The bedroom window should be in one of the walls adjacent
to the bedroom door
-
The bedroom window should be east to catch the morning light
-
What are the corresponding rules written in Prolog?
livingRoom(FD,BD,LW) :- opposite(FD,LW), adjacent(FD,BD).
// 1 and 2
bedroom(BD,BW) :- adjacent(BD,BW), BW=east. //
3 and 4
apartment(FD,LW,BD,BW) :- livingRoom(FD,LW,BD), bedroom(BD,BW).
-
What facts are required?
opposite(east,west).
opposite(north, south).
adjacent(east,south).
adjacent(east,north).
adjacent(west,south).
adjacent(west,north).
adjacent(north,east).
adjacent(north,west).
adjacent(south,east).
adjacent(south, west).
-
Is ?livingRoom(east, south, west) valid?
The answer is yes, since we can prove that opposite(east,west)
and adjacent(east,south) are true using our first prolog rule.
Procedural Meaning
-
Specifies how prolog answer questions
-
To answer a questions means to try and satisfy a list of
goals
-
Goals can be satisfied if the variables that occur in them
can be instantiated in such a way that the goals logically follow from
the program
-
The procedural meaning of Prolog is a procedure for executing
list of goals with respect to given program (the abstract interpreter)
| 8.2
Programming with Relations |
Example
-
The staff of an office run a coffee club, and they have set
up a database containing the following relations:
manager(NAME) which is true if NAME is a manager
bill(NAME,NUMBER,AMOUNT), which is true if NAME has been
sent a bill number NUMBER for AMOUNT
paid(NUMBER,AMOUNT,DATE), which is true if a payment
of AMOUNT was made on DATE for the bill numbered NUMBER
before(A,B), which is true if date A is before date B
-
How would you write queries for the following questions?
Which managers have been sent a bill for less the 10 dollars?
?manager(NAME), bill(NAME,NUMBER, AMOUNT), AMOUNT <
10.
Who has been sent more than one bill?
?bill(NAME, NUMBER1, AMOUNT1), bill(NAME, NUMBER2, AMOUNT2),
NUMBER1 \= NUMBER2.
Who has made a payment that is less than the amount
of their bill?
?bill(NAME, NUMBER, AMOUNT1), paid(NUMBER, AMOUNT2, DATE),
AMOUNT2 < AMOUNT1.
Who has received a bill and either not paid it at
all, or not paid it before Feb 1st?
?paid(NUMBER,AMOUNT, DATE), before(DATE, feb1).
Example
-
Consider the relations uses(Person,Program,Machine) identifying
a person runs a program on a specific machine and needs(Program, Memory)
identifying how much memory a program requires
-
We can fill in our databases with specific clauses such as
the following:
uses(dwight, compiler, sun).
uses(dwight, compiler, pc).
uses(dwight, compiler, mac).
uses(dwight, editor, sun).
uses(anna, editor, mac).
uses(jane, database, pc).
needs(compiler,128).
needs(editor, 512).
needs(database, 8192).
-
How would you write queries for the following questions?
What program needs more than 256k memory?
?needs(Program, Memory), Memory > 256.
What program does each person use?
?uses(Person, Program, Machine).
Which programs are used by two different people on
the same machine?
?uses(Person1, Program, Machine), uses(Person2,
Program, Machine), Person1 \= Person2.
What people use what programs on what machines with
what memory? // A Relational Join
?uses(Person, Program, Machine), needs(Program,
Memory).
What programs do both Anna and Jane use? // A Relational
Intersection
?uses(anna, Program, Machine), uses(jane, Program,
Machine).
Syntax
-
atom = many, can_steal, e.g., symbol beginning with
a lower case letter
-
integer = 999, 666, etc.
-
Constant = atom | integer
-
Variable = any symbol beginning with uppercase letter or
just a simple underscore.
-
Term = constant | variable | structure
-
Structure = functor + zero or more terms
e.g. owns(john, book(interview_with_vampier, author(anna,
rice)))
Operators
Arithmetic
-
The term x + y * z can be expressed as +(x, *(y,z)), either
is ok
-
However, remember operators do not cause any arithmetic do
be done
-
3 + 4 is just the term +( 3, 4)
X + Y
X - Y
X * Y
X / Y
X mod Y
Equality and Matching
X = Y // succeeds when both X and Y are uninstantiated,
when one is bound and the other is not, or both match
X \= Y
X < Y
X > Y
X =< Y
X >= Y
X is Y // succeeds with both X and Y are uninstantiated
or if X is an unbound variables and it is then bound to the term bound
to Y
-
A unifier of two terms is a substitution making the terms
identical
-
For example, append([1,2,3], [3,4], LIST1) and append(LIST2,
[3,4], [5,6]) unify
-
A unification algorithm computes the most general unifier
of two terms, if it exists, and reports failure otherwise.
-
The most general unifier of two terms is a unifier such that
the associated common instance is most general
-
If two terms unify, the there is a unique most general unifier
-
Unification Algorithm:
Input: Two terms T1 and T2 to be unified
Output: Q, the most general
unifier of T1 and T2, or failure
Algorithm:
Initialize the substitution of Q
to be empty,
the stack to contain the equation T1=T2,
and failure to false
While Stack not empty and no failure do
pop X=Y from the stack
Case
X is a variable that does not occur in Y:
Substitute Y for X in the stack and in Q
add Y=X to Q
Y is a variable that does not occur in X:
Substitute X for Y in the stack and in Q
add Y=X to Q
X and Y are identical constants or variables:
X is f(X1, ..., Xn) and Y is (Y1, ...., Yn)
for some function f and n>0:
push Xi=Yi, i=1, ...,n on the stack
otherwise:
end Case
end While
if failure, then output failure
else output Q
Matching Rules
-
Any uninstantiated variables matches any object, including
another variable. Therefore, the object will be bound to a variable
-
Integer or atoms only match with themselves
-
Structures will match with other structures with the same
functor and number of arguments with all arguments matching
Examples
| Term 1 |
Term 2 |
Does Term 1 unify/match with Term 2? |
| policeman |
policeman |
yes |
| paper |
pencil |
no |
| 1066 |
1066 |
yes |
| 1206 |
1583 |
no |
| rides(clergyman bicycle) |
rides(clergyman, X) |
yes with X bound to bicycle |
| a(b,c,d(e,F,g(h,i,J)) |
a(B,c,d(E,f,g(H,i,j)) |
yes with B bound to b, E bound to e, F bound to f, H,
bound to h, and J bound to j |
-
Prolog performs a task in response to your questions
-
A question provides a conjunction of goals to satisfy
-
Prolog uses known clauses to satisfy goals
-
A fact causes goal to be satisfied immediately
-
A rules can only reduce the task to that of satisfying subgoals
-
However, a clause can only be satisfied if it matches the
goal under consideration
-
If goal cannot be satisfied, backtracking occurs
-
Backtracking consists of reviewing what has been done and
attempting to re-satisfy the goals by finding an alternative to satisfy
them
-
Consider the following database
likes(mary,food).
likes(mary, wine).
likes(john,wine).
likes(john,marry).
likes(paul, marry).
?likes(X,mary). // question
x = john; //; says try again
x= paul;
no
What about ?likes(mary, X), likes(john,X).
-
first goal succeeds with x = food,
-
try second goal likes(john, food)
-
second goal fails, forget x and backtrack to re-satisfy goal
-
first goal succeed with x = wine,
-
try second goal likes(john, wine)
-
second goal succeeds
-
Prolog tells you of success
-
empty list is known as []
-
a list normally has a head and a tail - just like Scheme
-
[a] is equivalent to .(a,[]), where . is the functor
-
Therefore, .(a, .(b, .(c,[]))) is the same as [a,b,c] - the
same as Scheme's consing behavior
-
Legal lists include the following:
-
[]
-
[the, men, [like, to, fish]]
-
[a,V1, b, [X, Y]]
-
Manipulate lists by splitting the head and the tail [X |
Y], X represents head of list, Y represents the tail, which is a list
-
For example
-
If we have the fact p([1,2,3]), then the query ?p(X |Y) would
succeed with X bound to 1 and Y bound to [2,3]
-
If we have the fact p([the, cat, sat, [on, the, mat]], then
the query ?p(_,_,_,[_|X]] would succeed with X bound to [the,mat]
-
How to lists unify?
| List1 |
List2 |
Unification of List1 and List2 |
| [X,Y,Z] |
[john,likes,fish] |
X bound to john, Y bound to likes, Z bound to fish |
| [cat] |
[X|Y] |
X bound to cat, Y bound to [] |
| [X, Y|Z] |
[mary, likes, wine] |
X bmound to mary, Y bound to likes, Z bound to [wine] |
| [[the, Y] | Z] |
[[X, hare], [is , here]] |
X bound to the, Y bound to hare, Z bound to [[is, here]] |
Programming with Lists
Member relation member(X, Y). Is X a member of the
list Y
member(X, [X|_]).
member(X,[_|Y]) :- member(X,Y).
-
Prolog responds to questions
-
Questions provides conjunction of goals to be satisfied
-
Prolog uses clauses to satisfy goals
-
Clauses only used if they match/unify with goal
-
if can't satisfy goal, backtrack
-
Backtracking attempts to review and re-satisfy goals
