95.501

2000

2 Scheme Introduction

What's in This Set of Notes ?

Lisp and Scheme
Expressions
Naming and Environments
Evaluating Combinations
Compound Procedures
Substitution Model for Procedure Application

2.1 Lisp and Scheme

Lisp (LISt + Processing)

invented late 1950's
formalism for reasoning about the use of recursive equations as a model of computation
John McCarthy's paper: "Recursive Functions of Symbolic Expressions and Their Computation by Machine"

Scheme

dialect of Lisp
invented in 1975 by Guy Steele and Gerald Sussman, MIT
IEEE Standard in 1990

Important feature

processes, called procedures, can be manipulated as data

2.2 Expressions

present interpreter expression, it displays result of its evaluation
Numbers

486 => 486

Variables

dog => 2

expression with numbers combined with expression representing primitive procedure form Compound Expression

(+ 4 1) => 5

(- 4 1) => 3

(* 4 5) => 20

(/ 10 5) => 2

(+ 2.7 10) => 12.7

Expression like these when delimited with parentheses to denote procedure application are called combinations

(operator operand1 operand2 ..)

prefix notation
advantages

many operands possible

(+ 21 35 12 7) => 75

allows combinations to be nested

(+ ( * 3 5) (- 10 6)) => 19

no limit

( + ( * 3 ( + ( * 2 4) (+ 3 5))) (+ ( - 10 7) 6))

with help from formatting

( + ( * 3

( + ( * 2 4)

(+ 3 5)))

(+ ( - 10 7) 6))

2.3 Naming and Environments

Name identifies a variable whose value is object
Name binds a variable to a computational object

(define size 2) size => 2

(* 5 size) => 10

(define pi 3.14159)

(define radius 10)

(define circumference ( * 2 pi radius))

circumference => 62.8318

Interpreter must maintain name-object pairs
This memory is called the environment (global environment)

2.4 Evaluating Combinations

Evaluation Rule

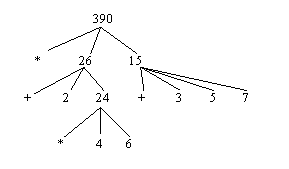
evaluate subexpressions of combination
apply procedure to resulting arguments

Note, the approach is recursive

(* ( + 2 ( * 4 6))

(+ 3 5 7))

Terminals: operators or numbers
Nodes: combinations
the values of numerals are the numbers that they name
the values of built-in operators ar the machine instructions sequences that carry out the corresponding operations
the values of other names are the objects associated with the names in the environment

Problem: evaluation rule does not handle definitions

(define x 3) does not apply define to two arguments, one of which is the symbol x, the other of which is 3)

Exceptions to general evaluation rules are called special forms

have own evaluations rules

2.5 Compound Procedures

What elements in Scheme must appear in any powerful programming language?

Numbers and arithmetic operations are primitive data and procedures
Nesting of combinations provides a means of combining operations
Definitions that associates names with values provides a limited means of abstractions

Procedure Definitions

Abstraction technique
Operations given name and referred to as a unit
General form: (define (<name> <formal parameters>) <body>)

(define (square x) (* x x))

(square 21) => 441

(square ( + 2 5)) => 49

suppose we want x squared plus y squared

(+ (square x) (square y))

(define (sum-of-squares x y)

(+ (square x) (square y)))

(sum-of-squares 3 4) => 25

What is the answer to the following:

(define (f a)

(sum-of-squares (+ a 1) (* a 2)))

(f 5) => 136

2.6 Substitution Model for Procedure Application

Think about procedure application

Determines "meaning" of procedure application

Applicative-Order evaluation (Scheme approach)

evaluate operator and operands
apply the resulting procedure to resulting arguments

(f 5)

(sum-of-squares (+ 5 1) (* 5 2))

(+ (square 6) (square 10))

(+ ( * 6 6 ) (* 10 10))

(+ 36 10)

136

Normal-Order evaluation (expand and reduce)

substitute operand expressions for parameters until reaching primitive operators,
then evaluate

(f 5)

(sum-of-squares (+ 5 1) (* 5 2))

(+ (square (+ 5 1)) (square (* 5 2)))

(+ ( * (+ 5 1) (+ 5 1) ) (* (* 5 2) (* 5 2)))

(+ (* 6 6) ( * 10 10))

(+ 36 10)

136

Which evaluation technique is Better?

both approaches result in the same answer

applicative-order evaluation is more efficient -> avoid multiple evaluations

normal-order also has benefits, will see later