Consider a Marketplace consisting of N consumers and L different commodities. Each consumer i has an initial endowment vector wi of L commodities. Only activities that consumers can perform is to consume and/or trade their commodities (no production is allowed - only pure exchanges). Each consumer has h(er/is) own preferences, described using a utility function u. Let us say that given a vector of quantities of L commodities, the utility function for a given user maps it to a positive real number. Objective of each of the consumers is to maximize their utility by performing pure exchanges of the given commodities. There are natural constraints that the consumers must satisfy. The wealth of a consumer is h(er/is) initial endowment, and the total amount of commodities that a consumer can acquire (or buy) is at most equal to h(er/is) initial wealth (i.e. the commodities that the consumer sells off). The problem we want to address is how to figure out how the exchanges be performed so that each consumer increases the utility? Also is there an equilibrium, an optimum value for each consumer, so that no further exchanges benefit consumers as a whole (only way to increase utility of a consumer is by decreasing the utility of another). To add to complications, the utility functions are private, otherwise the consumers will tend to lie!
To solve this problem, prices are set for each of the
commodities. (Call this the price vector p.) Now the consumer i buys
the vector of commodities xi, such that its utility ui(xi) is
maximized subject to the constraint that amount that the agent pays
for acquiring the commodities xi is at most the amount the agent
received for h(er/is) initial endowment (i.e.
![]() ). We
solve this maximization problem for each of the consumers. With a
given price vector it is possible that the market may not clear.
There may be excess demand for certain commodities. In that case the
price of that commodity will be raised. The market will clear if all
the commodities have been purchased (i.e. sum total of the demand for
a commodity equals the sum total of the initial endowment of that
commodity, namely Walras Law). Now we need to worry about whether can
we find a price vector such that the market clears? We will formalize
all this and state and prove the equilibrium theorem.
). We
solve this maximization problem for each of the consumers. With a
given price vector it is possible that the market may not clear.
There may be excess demand for certain commodities. In that case the
price of that commodity will be raised. The market will clear if all
the commodities have been purchased (i.e. sum total of the demand for
a commodity equals the sum total of the initial endowment of that
commodity, namely Walras Law). Now we need to worry about whether can
we find a price vector such that the market clears? We will formalize
all this and state and prove the equilibrium theorem.
Let consumer i's endowment vector be wi= (wi1, wi2, ..., wiL), and ui be its utility function corresponding to the locally non-satiated preference relation. Denote consumer i's excess demand vector for any given distribution of endowments as zi(p), where
The vector of aggregate excess demands Z(p), can be described as follows:
The Walrasian equilibrium in this pure exchange economy will be that
price vector p* and allocation x*, such that all markets clears,
i.e. Z(p*)=0. It turns out that the demand for each consumer xi
will be such that the budget constraint will be binding, i.e.,
p*.xi = p*.wi (Walras Law). Summing up these budget constraints
for all consumers gives us
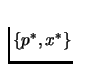 be a Walrasian Equilibrium then
be a Walrasian Equilibrium then
Proof:
Walras Law implies that
p*.Z(p*) = 0, i.e.,
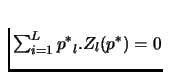 .
Note that
.
Note that
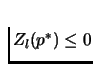 .
We will show that
.
We will show that
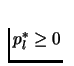 for all
l=1,...,L. Hence the lemma follows.
for all
l=1,...,L. Hence the lemma follows.
To show that
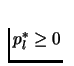 ,
for all l=1,..,L, assume that its not
true for at least one value of l. Then its easy to see that the
utility maximization problem will have no solution (an unbounded
value).
,
for all l=1,..,L, assume that its not
true for at least one value of l. Then its easy to see that the
utility maximization problem will have no solution (an unbounded
value).
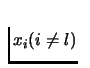 can be increased unboundedly, and
hence the utility can be increased unboundedly, a contradiction to the
existence of an optimum.
can be increased unboundedly, and
hence the utility can be increased unboundedly, a contradiction to the
existence of an optimum.
Furthermore, we assume that Z(p) satisfies the following:
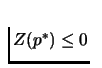 .
.Proof: The main idea of the proof is the following. Prices will be normalized and restricted to an L-dimensional simplex. If there is an excess demand for a commodity, then its price will be raised and the other prices will be normalized so that they are restricted to simplex. Simplex is compact and convex. It turns out that this process is a continuous mapping of points in simplex to points in simplex, and satisfies all the properties required in Brouwer's fix point theorem. This implies that there is a price vector, which corresponds to the fix point. We will prove that this price vector is a Walrasian Equilibrium Price Vector.
Let
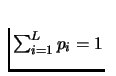 .
Define
.
Define
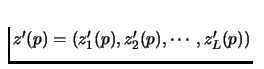 ,
where
,
where
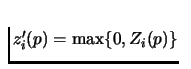 .
The new price vector
.
The new price vector
![]() is given by
is given by
 is some normalization constant. It turns out the
is some normalization constant. It turns out the
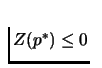 .
.