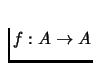 a continuous
function. Then f has a fix point, i.e. f(x)=x for some
a continuous
function. Then f has a fix point, i.e. f(x)=x for some 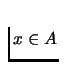 .
.
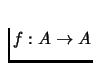 a continuous
function. Then f has a fix point, i.e. f(x)=x for some
a continuous
function. Then f has a fix point, i.e. f(x)=x for some 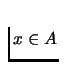 .
.Let us define the terms which are used in the theorem:
A set
![]() is compact if it is bounded and closed
relative to Rn. A set A is bounded if there is some
is compact if it is bounded and closed
relative to Rn. A set A is bounded if there is some 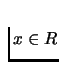 ,
such that ||a|| < x for all
,
such that ||a|| < x for all 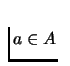 .
Moreover, if f is a
continuous function, then it maps compact sets to compact sets.
.
Moreover, if f is a
continuous function, then it maps compact sets to compact sets.
Let the sequence xm converge to x in Rn. Point x is the
limit point of the sequence. Let
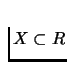 be the domain of the
function f. The function f is said to be continuous if for
all
be the domain of the
function f. The function f is said to be continuous if for
all 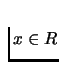 ,
and every convergent sequence xm to x, f(xm)
converges to f(x). A set is open, if for every point in the
set, we can find a small neighborhood, such that all points in the
neighborhood are within the set. A set is closed, if its
complement is open.
,
and every convergent sequence xm to x, f(xm)
converges to f(x). A set is open, if for every point in the
set, we can find a small neighborhood, such that all points in the
neighborhood are within the set. A set is closed, if its
complement is open.
Lets first look at the Brouwer's theorem in one dimension. Let f be
a continuous function in the interval
![$f:[0,1] \rightarrow [0,1]$](img9.gif) .
We
want to show that there exists
.
We
want to show that there exists
![$x\in [0,1]$](img10.gif) such that f(x)=x (see Figure 2.
Assume that f(0) and f(1) are not equal to 0 and 1,
respectively, otherwise we already have a fix-point. Plot this
function on the x-y plane, restricted to the interval
[0,1]x[0,1]. Consider the plot of this function and the line
x=y. Clearly these two intersects in at least one point, since f
starts above this line at x=0, and terminates below this line at
x=1, and is continuous. All intersection points are fix points!
such that f(x)=x (see Figure 2.
Assume that f(0) and f(1) are not equal to 0 and 1,
respectively, otherwise we already have a fix-point. Plot this
function on the x-y plane, restricted to the interval
[0,1]x[0,1]. Consider the plot of this function and the line
x=y. Clearly these two intersects in at least one point, since f
starts above this line at x=0, and terminates below this line at
x=1, and is continuous. All intersection points are fix points!
Proof in two and higher dimensions uses Sperner's Lemma. (This proof is based on the survey paper of P.J.S.G. Ferreira on Fixed point problems - an introduction).
We want to show that a continuous mapping from a closed triangle T
(or circle) to a closed triangle has a fixed point. Since T is
convex, any point in T can be expressed using the barycentric
coordinates
(a0, a1, a2), such that
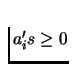 and
a0+a1+a2=1. The function f maps points in T to points in
T, i.e.,
f(a0,a1,a2)=(b0,b1,b2) where all points are
represented using the barycentric coordinates.
and
a0+a1+a2=1. The function f maps points in T to points in
T, i.e.,
f(a0,a1,a2)=(b0,b1,b2) where all points are
represented using the barycentric coordinates.
(What are Barycentric coordinates? For any point x inside a triangle ABC, there exists three weights wA, wB, and wC such that, if placed at the corresponding vertices of the triangle, their center of gravity (barycenter) will coincide with the point x. August Ferdinand Moebius (1790-1868) defined the weights wA, wB, and wC as the barycentric coordinates of x, provided wA+wB+wC =1. )
Define three sets Si of points, where i=0,1,2, such that
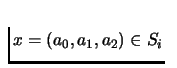 if
if
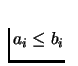 .
Observe that the vertex
.
Observe that the vertex
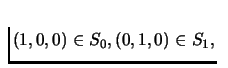 and
and
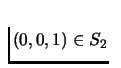 .
We will show that
the points belonging to the intersection of these three sets are fixed
points! Suppose the intersection is non-empty and let
x=(a0, a1,
a2) be such a point, with its image
f(x)=(b0,b1,b2). By
definition
.
We will show that
the points belonging to the intersection of these three sets are fixed
points! Suppose the intersection is non-empty and let
x=(a0, a1,
a2) be such a point, with its image
f(x)=(b0,b1,b2). By
definition
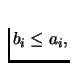 for i=0,1,2. But
a0+a1+a2=1=b0+b1+b2, hence x=f(x). Next we show that the
intersection of these sets is non-empty! That's where the Sperner's
lemma will be used.
for i=0,1,2. But
a0+a1+a2=1=b0+b1+b2, hence x=f(x). Next we show that the
intersection of these sets is non-empty! That's where the Sperner's
lemma will be used.
First of all vertices of the triangle can be labeled by 0, 1 and
2, respectively because of the following. Let (1,0,0) be a vertex
and let
f(1,0,0)=(b0,b1,b2). Clearly 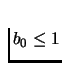 ,
and hence this
vertex can be labeled by 0. Next consider a point x on one of the
sides of T, say defined by vertices labeled 0 and 1.
Barycentric coordinate of point x will be
(a, 1-a, 0), where
,
and hence this
vertex can be labeled by 0. Next consider a point x on one of the
sides of T, say defined by vertices labeled 0 and 1.
Barycentric coordinate of point x will be
(a, 1-a, 0), where
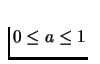 .
Consider f(x)=y. Now y may be mapped to the same edge
of the triangle or somewhere else. First consider the case that y
is mapped to the same edge as x. Now barycentric coordinate of
y=(b,1-b, 0) where
.
Consider f(x)=y. Now y may be mapped to the same edge
of the triangle or somewhere else. First consider the case that y
is mapped to the same edge as x. Now barycentric coordinate of
y=(b,1-b, 0) where
![]() .
If
.
If 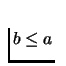 ,
then label of point
x will be 0 otherwise it will be 1. What about if point y is
not on this edge? Then the third coordinate of y is non-zero, but
the third coordinate of x is zero. This implies that x cannot be
labeled 2. So the points along this edge of the triangle will be
labeled 0 or 1, as required in Sperner's lemma.
,
then label of point
x will be 0 otherwise it will be 1. What about if point y is
not on this edge? Then the third coordinate of y is non-zero, but
the third coordinate of x is zero. This implies that x cannot be
labeled 2. So the points along this edge of the triangle will be
labeled 0 or 1, as required in Sperner's lemma.
Next we show that the sets Si are closed. Consider a convergent
sequence xn of points in Si and let x be the limit of the
sequence. Why is 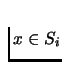 ? Let
xn=(a0n, a1n, a2n) and
the image
yn=f(xn)=(b0n, b1n, b2n). Moreover
? Let
xn=(a0n, a1n, a2n) and
the image
yn=f(xn)=(b0n, b1n, b2n). Moreover
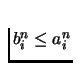 by definition of Si. Since f is a continuous function, so
the coordinates ai and bi of the limit point a and f(x) will
satisfy the similar condition and hence
by definition of Si. Since f is a continuous function, so
the coordinates ai and bi of the limit point a and f(x) will
satisfy the similar condition and hence 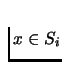 .
.
By Sperner's Lemma, if we consider a subdivision of T, then there is a baby triangle with vertices 0,1, and 2, and this baby triangle can be very very small! This implies that the points of the sets S0, S1 and S2 become arbitrary close in this baby triangle of very very small diameter. But sets Si are closed and non-empty - this implies they should eventually intersect!