


Next: Competitive Equilibrium
Up: Models, Algorithms and Economics
Previous: Brouwer's Fix Point Theorem
Definitions of Economics Terms
These are taken from the book [#!MWG95!#].
- Preference Relations:
- A relation that captures the decision makers taste! Its a usual
binary relation, denoted by
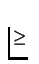 (greater than equal to) on the
set X, where X denotes the set of alternatives. A rational
preference relation is the one which is complete and
transitive. By complete we mean that any two elements in the set
X are comparable.
(greater than equal to) on the
set X, where X denotes the set of alternatives. A rational
preference relation is the one which is complete and
transitive. By complete we mean that any two elements in the set
X are comparable.
- Utility Functions:
- A utility function assigns a numerical value to each element of
the set X (i.e. the set of choices/alternatives). If
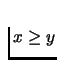 ,
then
,
then
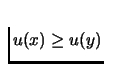 ,
where
,
where
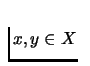 .
Here it is assumed
that there is a rational preference relation on the set X, and
the utility function preserves that preference relation.
.
Here it is assumed
that there is a rational preference relation on the set X, and
the utility function preserves that preference relation.
- Commodities:
- The objects of choice by consumers in a market economy.
Commodities are finite in number. The commodity vector represents
amounts of different commodities, usually referred to as a
consumption bundle/vector. Let us assume that there are in all
L different commodities. Consumption set is a subset of the
commodity space RL, where each element of the subspace is a
consumption bundle.
- Who is Walras?
- Here is a great web-site about Who is
Walras
and on his Contributions to
Economics.
- Walrasian Set/ Competitive Budget Set:
- Assume that each commodity has a given price (per unit). The
consumption bundle
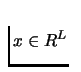 is affordable for a consumer if its
total cost does not exceed the wealth of the consumer w (i.e.,
is affordable for a consumer if its
total cost does not exceed the wealth of the consumer w (i.e.,
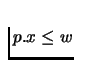 ). The Walrasian set or the competitive budget set
refers to the set of affordable consumption bundles (i.e.,
). The Walrasian set or the competitive budget set
refers to the set of affordable consumption bundles (i.e.,
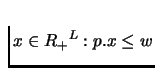 ).
).
- Walrasian demand function:
- For each price wealth pair, (p,w), x(p,w) refers to the set of
consumption bundles satisfying (p,w). In general x(p,w) is a
relation, but in the case it is single valued, it is called a
demand function, otherwise demand correspondence. Walrasian
demand correspondence is homogeneous of degree zero if for any
constant
r >0, x(rp, rw)=x(p,w) (i.e. scaling of price and
wealth by the same proportion does not alter the choices for the
consumers).
- Walras's Law:
- Walrasian demand correspondence satisfies Walras's Law if for
every p and w >0, p.x = w, for all
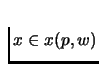 .
Essentially it says that consumers fully expends their wealth!
.
Essentially it says that consumers fully expends their wealth!
- Monotone preference relation:
- A preference relation on X is monotone, if
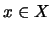 ,
and
,
and 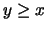 ,
then
,
then 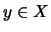 (consumption of larger amounts of goods is
always feasible).
(consumption of larger amounts of goods is
always feasible).
- Non-satiated preference relation:
- For every
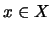 ,
and every
,
and every
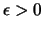 ,
there is a
,
there is a 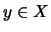 ,
such that
,
such that
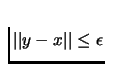 and
and 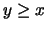 .
(Always in the
neighborhood of x, we can find another consumption bundle y,
that is preferred over x, and y is not same as x.)
.
(Always in the
neighborhood of x, we can find another consumption bundle y,
that is preferred over x, and y is not same as x.)
- Convex preference relation:
- A preference relation is convex, if for every
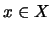 ,
the set
,
the set
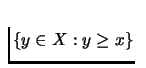 is convex (upper contour set is convex).
is convex (upper contour set is convex).
- Continuous preference relation:
- It is continuous if it is preserved under limits. For any sequence
of pairs
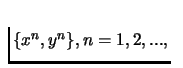 with
with
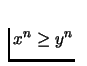 ,
and
,
and
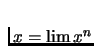 and
and
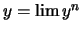 ,
when
,
when
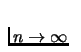 ,
then
,
then 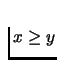 .
Alternatively, the upper contour set
.
Alternatively, the upper contour set
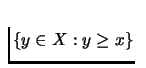 ,
and the lower contour set
,
and the lower contour set
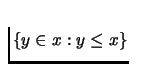 are
closed. Consumer preferences do not exhibit jumps!! It turns out
that for every continuous preference relation, one can find a
continuous utility function!
are
closed. Consumer preferences do not exhibit jumps!! It turns out
that for every continuous preference relation, one can find a
continuous utility function!
- Utility maximization problem:
- Assume that consumers have rational, continuous, and locally
non-satiated preference relation over the set X=R+L and the
corresponding continuous utility function u(x). Then the
maximization problem is to max u(x), subject to
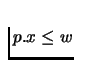 and
and
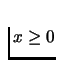 .
Why does utility maximization problem has a solution?
Note that continuous functions always have an optimum value on a
compact set. Utility function is continuous. The set of feasible
solutions, namely the budget set,
.
Why does utility maximization problem has a solution?
Note that continuous functions always have an optimum value on a
compact set. Utility function is continuous. The set of feasible
solutions, namely the budget set,
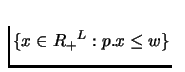 is
compact, since it is bounded and closed.
is
compact, since it is bounded and closed.



Next: Competitive Equilibrium
Up: Models, Algorithms and Economics
Previous: Brouwer's Fix Point Theorem
Anil Maheshwari
2003-03-05
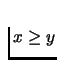 ,
then
,
then
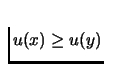 ,
where
,
where
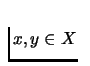 .
Here it is assumed
that there is a rational preference relation on the set X, and
the utility function preserves that preference relation.
.
Here it is assumed
that there is a rational preference relation on the set X, and
the utility function preserves that preference relation.
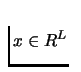 is affordable for a consumer if its
total cost does not exceed the wealth of the consumer w (i.e.,
is affordable for a consumer if its
total cost does not exceed the wealth of the consumer w (i.e.,
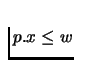 ). The Walrasian set or the competitive budget set
refers to the set of affordable consumption bundles (i.e.,
). The Walrasian set or the competitive budget set
refers to the set of affordable consumption bundles (i.e.,
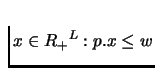 ).
).
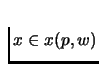 .
Essentially it says that consumers fully expends their wealth!
.
Essentially it says that consumers fully expends their wealth!
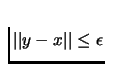 and
and 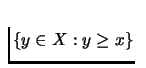 is convex (upper contour set is convex).
is convex (upper contour set is convex).
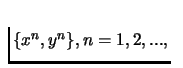 with
with
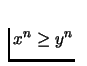 ,
and
,
and
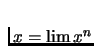 and
and
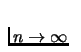 ,
then
,
then 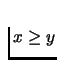 .
Alternatively, the upper contour set
.
Alternatively, the upper contour set
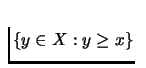 ,
and the lower contour set
,
and the lower contour set
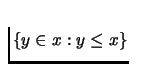 are
closed. Consumer preferences do not exhibit jumps!! It turns out
that for every continuous preference relation, one can find a
continuous utility function!
are
closed. Consumer preferences do not exhibit jumps!! It turns out
that for every continuous preference relation, one can find a
continuous utility function!
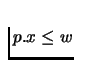 and
and
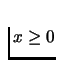 .
Why does utility maximization problem has a solution?
Note that continuous functions always have an optimum value on a
compact set. Utility function is continuous. The set of feasible
solutions, namely the budget set,
.
Why does utility maximization problem has a solution?
Note that continuous functions always have an optimum value on a
compact set. Utility function is continuous. The set of feasible
solutions, namely the budget set,
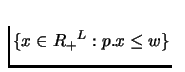 is
compact, since it is bounded and closed.
is
compact, since it is bounded and closed.