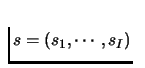 constitutes a
Nash Equilibrium if for every
constitutes a
Nash Equilibrium if for every
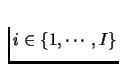
First consider only pure strategies (no randomization or mixed
strategies). A strategy profile
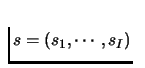 constitutes a
Nash Equilibrium if for every
constitutes a
Nash Equilibrium if for every
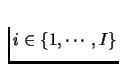
![]() for all
for all
![]() .
Which
strategy profile constitutes a Nash Equilibrium in the following game?
.
Which
strategy profile constitutes a Nash Equilibrium in the following game?
| y1 | y2 | y3 | |
| x1 | 1,4 | 2,2 | 2,3 |
| x2 | 3,1 | 1,5 | 4,1 |
| x3 | 2,0 | 3,4 | 1,2 |
If Player 2 plays y2, then the best response of player 1 is
x3. If player 1 plays x3, then the best response of player 2 is
y2. This implies that strategy profile (x3,y2) is a Nash
Equilibrium. What if player 2 plays y1, then player 1's best
response is x2, but for x2, player 2's best response is
y2. Similarly if player 2 plays y3, then player 1's best
response is x2, but for x2, player 2's best response is
y2. Therefore
![]() is the only Nash Equilibrium strategy
profile.
is the only Nash Equilibrium strategy
profile.
Consider the game of Matching Pennies.
| Heads | Tails | |
| Heads | -1, 1 | 1, -1 |
| Tails | 1, -1 | -1, 1 |
Observe that there is no pure strategy equilibrium in the Matching Pennies.
When does (pure strategy) Nash Equilibrium exists?
(We are following the treatment in the book [#!OR94!#].)
First we need a few definitions and Kakutani's fixed point theorem.
For any player i, define the best response correspondence
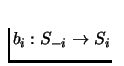 such that for each
such that for each
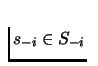 ,
the set
,
the set
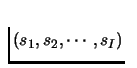 is Nash Equilibrium if and only if each
is Nash Equilibrium if and only if each
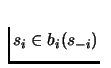 .
Define the correspondence
.
Define the correspondence
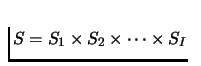 .
.
A correspondence
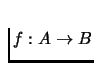 ,
where
,
where
![]() ,
the set
,
the set
![]() is closed, has a closed graph if for any two converging
sequences,
is closed, has a closed graph if for any two converging
sequences,
![]() and
and
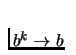 ,
where
,
where
![]() and
and
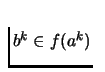 for all k, then
for all k, then 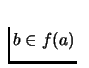 .
The
correspondence
.
The
correspondence
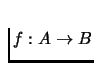 ,
where B is closed, is upper
hemicontinuous if it has a closed graph and the images of the compact
sets are bounded. A function
,
where B is closed, is upper
hemicontinuous if it has a closed graph and the images of the compact
sets are bounded. A function
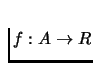 defined on a convex
set
defined on a convex
set
![]() is quasi-concave if its upper contour set
is quasi-concave if its upper contour set
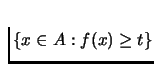 ,
for some value t is convex.
,
for some value t is convex.
Here is the fixed point theorem due to Kakutani, and fir Illustration in one dimension see Figure 3.
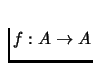 be a upper hemicontinuous correspondence
from A to itself, such
that
be a upper hemicontinuous correspondence
from A to itself, such
that 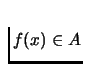 is nonempty and convex for each
is nonempty and convex for each 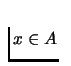 .
Then f
has a fixed point, i.e.
.
Then f
has a fixed point, i.e. 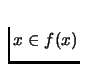 for some
for some 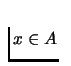 .
.
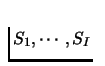 are nonempty, Si is compact and
convex, and the utility function is continuous, and quasi-concave in
each of the variables si, then the function bi is nonempty,
convex-valued, and upper hemicontinuous.
are nonempty, Si is compact and
convex, and the utility function is continuous, and quasi-concave in
each of the variables si, then the function bi is nonempty,
convex-valued, and upper hemicontinuous.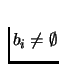 .
The set bi is convex, since the set of
maximizers of a quasi-concave function on a convex set are convex.
For upper hemicontinuity, we need to show that for any sequence
.
The set bi is convex, since the set of
maximizers of a quasi-concave function on a convex set are convex.
For upper hemicontinuity, we need to show that for any sequence
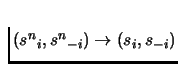 such that
such that
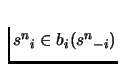 ,
,
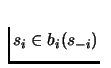 .
For all n,
.
For all n,
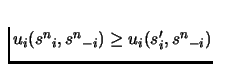 for all
for all
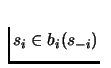 .
.
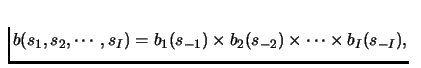 where
where
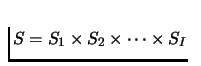 .
From Lemma 2 we know that bi()'s are
nonempty, convex-valued and upper hemicontinuous. Now all the
conditions for Kakutani's fixed point theorem are satisfied by the
function b. Therefore there exists a fixed point for this
correspondence, say
.
From Lemma 2 we know that bi()'s are
nonempty, convex-valued and upper hemicontinuous. Now all the
conditions for Kakutani's fixed point theorem are satisfied by the
function b. Therefore there exists a fixed point for this
correspondence, say  ,
such that
,
such that  .
Clearly s is a
Nash Equilibrium since each
.
Clearly s is a
Nash Equilibrium since each
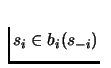 .
.
Of course this theorem applies when the sets Si are convex, but in our examples like Matching Pennies etc., the sets Si are finite! OOPS! Before we do the proofs for this scenario - lets introduce mixed strategy Nash Equilibrium.
A mixed strategy profile
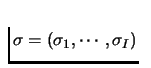 constitutes a Nash Equilibrium if for every
constitutes a Nash Equilibrium if for every
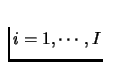 ,
,
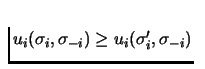 ,
for all
,
for all
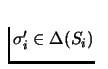 .
For example, consider the Matching Pennies game again. This game has
a mixed strategy equilibrium if each player chooses Heads or Tails
with equal probability. Although this game didn't have a pure strategy
Nash Equilibrium, but has a mixed strategy Nash Equilibrium! Here is
the celebrated Nash Theorem!
.
For example, consider the Matching Pennies game again. This game has
a mixed strategy equilibrium if each player chooses Heads or Tails
with equal probability. Although this game didn't have a pure strategy
Nash Equilibrium, but has a mixed strategy Nash Equilibrium! Here is
the celebrated Nash Theorem!
Proof:
Let player i, has M pure strategies in the set Si, i.e.,
|Si|=M. Recall the simplex
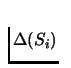 ,
representing the
probability vectors
,
representing the
probability vectors
In the following lemma we state an important property of mixed strategy Nash Equilibrium. It means that each player, given the distribution of strategies played by all his opponents, is indifferent among all pure strategies that (s)he plays. This lemma can be used to find the mixed strategy equilibrium.
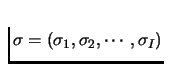 is an
equilibrium if and only if for every player
is an
equilibrium if and only if for every player 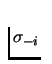 .
.
Proof:
Necessary: Suppose that there is a strategy
![]() in support of
in support of
![]() ,
but is not a best response to
,
but is not a best response to
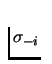 .
Then by the
linearity of the utility function ui, player i can increase
h(is/er) utility by transferring the probability from si to a
strategy, say s'i that is a best response (i.e. player i would
have played s'i in place of si and increased h(is/er) utility).
.
Then by the
linearity of the utility function ui, player i can increase
h(is/er) utility by transferring the probability from si to a
strategy, say s'i that is a best response (i.e. player i would
have played s'i in place of si and increased h(is/er) utility).
Sufficiency: Suppose that ![]() is not a Nash Equilibrium. Then
there is a player who has a strategy
is not a Nash Equilibrium. Then
there is a player who has a strategy ![]() with
with
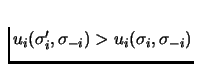 .
This implies
that there is a pure strategy
.
This implies
that there is a pure strategy
![]() such that
such that
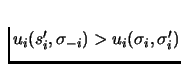 .
But by assumption
.
But by assumption
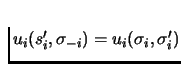 for all
for all
![]() which are played with positive probabilities.
which are played with positive probabilities. ![]()
What are Nash Equilibriums for the following game?
| Col-1 | Col-2 | |
| Row-1 | 2,2 | 3,4 |
| Row-2 | 1,3 | 5,1 |
Suppose Player 1 selects Row-1 and Row-2 with probability 1-p and
p respectively, i.e.
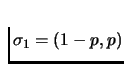 .
Then the utility of
Player 2, under strategy Col-1 and Col-2 should be the same, i.e.,
.
Then the utility of
Player 2, under strategy Col-1 and Col-2 should be the same, i.e.,
Similarly, if Player 2 selects Col-1 and Col-2 with probability
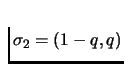 ,
then
,
then
Therefore Nash Equilibrium is
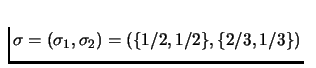 .
.
Here is a graphical way of computing Nash Equilibrium of  games.
In general let the game be given as follows:
games.
In general let the game be given as follows:
| 1-q | q | |
| 1-p | a1,b1 | a2,b2 |
| p | a3,b3 | a4,b4 |
Expected utility of the row player (Player 1) will be
First consider Player 1 (the row player). We can rewrite the utility
function u1 as a function of p, representing the equation of a
line
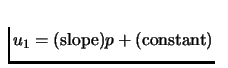 ,
as follows.
,
as follows.
The aim of the Player 1 is to maximize u1. In our example
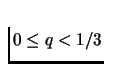 ,
p=0. For q=1/3,
,
p=0. For q=1/3,
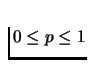 .
For
.
For
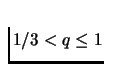 ,
p=1.
,
p=1.
Similarly aim of the Player 2 is to maximize u2. In our example
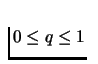 .
For
.
For 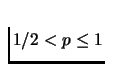 ,
q=0.
,
q=0.
The plots are shown in Figure 4, and the intersection of the two graphs, where p=1/2 and q=1/3 is the Nash Equilibrium in this case. These graphs can be viewed as ``no regrets graphs'' of the two players. Given the strategy of a player, the best strategy of the other player is the corresponding point on the graph. For example, if Player 1 chooses p=.2, then the best strategy for player 2 is to choose q=1 (or Player 2 has no regrets in choosing q=1).