![$\sigma_i:S_i \rightarrow
[0,1]$](img69.gif) such that for each pure strategy
such that for each pure strategy
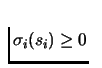 is assigned, that this strategy will be
taken. Moreover
is assigned, that this strategy will be
taken. Moreover
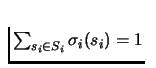 .
Observe that the
set of mixed strategies for a player forms a simplex. Let Si
consists of M pure strategies, then the Simplex is
.
Observe that the
set of mixed strategies for a player forms a simplex. Let Si
consists of M pure strategies, then the Simplex is
The definitions are from the book [#!MWG95!#]. A game consists of
players, rules, outcomes, and payoffs. The strategies of a
player are the decision rules that specify how a player will act in
every possible scenario. In other words, strategy is a function from
the set of scenarios to an action. A pure strategy (or deterministic)
specifies a fixed action, given a specific scenario. Let Si be the
set of pure strategies for the player i. A mixed strategy
(random) for a player i is a function
![$\sigma_i:S_i \rightarrow
[0,1]$](img69.gif) such that for each pure strategy
such that for each pure strategy
![]() ,
a probability
,
a probability
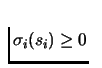 is assigned, that this strategy will be
taken. Moreover
is assigned, that this strategy will be
taken. Moreover
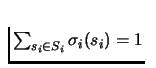 .
Observe that the
set of mixed strategies for a player forms a simplex. Let Si
consists of M pure strategies, then the Simplex is
.
Observe that the
set of mixed strategies for a player forms a simplex. Let Si
consists of M pure strategies, then the Simplex is
Denote by
![$\Gamma=[I,\{S_i\},\{u_i(.)\}]$](img74.gif) ,
the game with I players,
each with strategy set Si, and a payoff function
,
the game with I players,
each with strategy set Si, and a payoff function
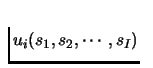 depending upon the outcomes arising from
strategies
depending upon the outcomes arising from
strategies
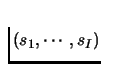 .
Profile for player i's opponent's is
denoted by
s-i=(s1, s2, ..., si-1, si+1, ..., sI).
.
Profile for player i's opponent's is
denoted by
s-i=(s1, s2, ..., si-1, si+1, ..., sI).
Consider the following game called Prisoner's Dilemma. In fact you can play a variant of this game on the web! See the following web-site. Two people are held as prisoners in separate cells for a possible involvement in a fraud. If both of them confess then they get 5 years in the prison. If one confesses and other doesn't then the first one gets 1 year and the other one 10 years, and if neither of them confess then each gets 2 years. Of course the objective of each of them is to minimize their time in the prison. Here is the payoff table (notice that the utility is the negative of the number of years in the prison).
| Prisoner 2 | |||
| Don't Confess | Confess | ||
| Don't Confess | -2, -2 | -10, -1 | |
| Prisoner 1 | |||
| Confess | -1, -10 | -5, -5 |
A strategy
![]() is called dominant for a player i if
for all
is called dominant for a player i if
for all
![]() ,
,
![]() .
In
the Prisoner's Dilemma example, the strategy (confess, confess) is
dominant! The reason is as follows: Considering Player 1. Let Player 2
plays Don't Confess. Then utility for Player 1 is highest by
playing Confess (-1 v/s -2). Similarly if Player 2 plays
Confess, then utility for Player 1 is highest by playing
Confess (-5 v/s -10). Therefore Confess is the dominant
strategy for Player 1. By symmetry, Confess is the dominant
strategy for Player 2, as well.
.
In
the Prisoner's Dilemma example, the strategy (confess, confess) is
dominant! The reason is as follows: Considering Player 1. Let Player 2
plays Don't Confess. Then utility for Player 1 is highest by
playing Confess (-1 v/s -2). Similarly if Player 2 plays
Confess, then utility for Player 1 is highest by playing
Confess (-5 v/s -10). Therefore Confess is the dominant
strategy for Player 1. By symmetry, Confess is the dominant
strategy for Player 2, as well.
Similarly we can define dominant mixed strategies for player i. A
strategy ![]() is a dominant strategy for player i if
is a dominant strategy for player i if
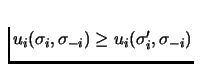 ,
for all
,
for all
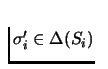 and
and
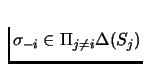 .
.