 |
Refer to this web site for this Lemma.
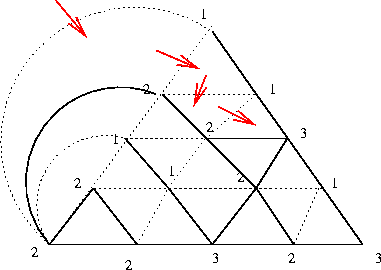
Divide a simplex (say a triangle in two dimension) into several, but finite, baby triangles. Make sure the triangulation is nice (i.e. two triangles only meet at a common edge or a vertex). Label the vertices of the simplex by 1, 2 and 3. Now label all the vertices on the side (12) by either 1 or 2. Similarly label all vertices on the side (23) by 2 or 3, and on side (13) by 1 or 3. Label the vertices in the interior arbitrarily by labels 1,2, or 3. No matter how you label following the rules, there is always an odd number of baby triangles with labels (123). Why?
Here is the proof: It is not hard to show the existence of at least one baby triangle with this property: First we add few triangles on the side (12), by joining each vertex on that side with the main vertex labeled 2. View the edges labeled as (12) as the doors into the simplex castle. We enter from outside the simplex through the edge (12) (see Figure 1). Now we can go to the neighboring triangle (i.e. a triangle sharing an edge) provided we have another edge labeled (12) (i.e. a door). We continue this traversal as long as as we can do that. Observe that the triangles encountered during our traversal have at most two edges labeled (12) - sort of one entry door and one exit door. So we cannot come back to the same triangle! But we cannot exit the simplex, since there is exactly one boundary edge labeled (12), the one which we entered! Since the triangulation is finite, that means that this walk ended in a triangle with exactly one edge labeled (12), and hence that is the baby triangle we are looking for with label (123).
(Alternatively, one can look at the dual of the triangulation, where the adjacency is defined with respect to whether the corresponding two triangles share a door. The dual graph has a simple and nice structure to prove everything which we need.) To prove that there are odd number of such triangles, start with the original simplex (without the extra edges which were added). Observe that there are odd number of boundary edges with label (12) (essentially the one dimensional problem). If we trace the path from these edges, we will terminate at odd number of required baby triangles with label (123). All other baby triangles with label (123) which are not reachable from these exterior edges come in pairs, and hence are even in number. Also this theorem generalizes to higher dimensions. (See the paper by Francis Edward Su : Rental harmony: Sperner's lemma in fair division. Amer. Math. Monthly, 106(1999), pp. 930-942.)